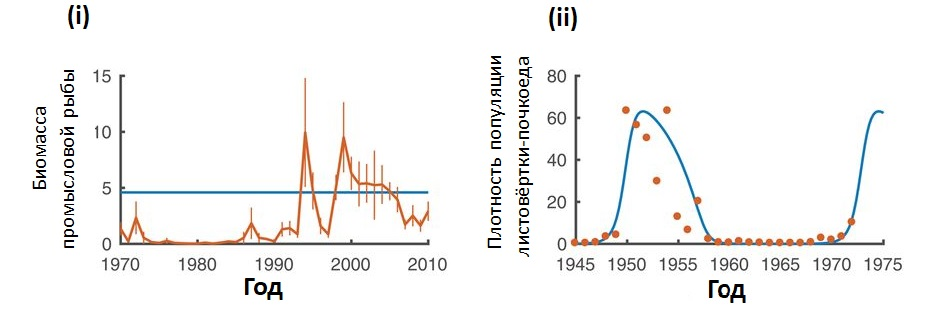
Математические модели в экологии традиционно акцентировали внимание на асимптотической или долгосрочной динамике, например, на изучении положений равновесия. Однако значительное количество недавних исследований показывает важность изучения динамики переходных процессов в экологических системах, в частности, рассмотрения длительных переходных процессов, которые могут продолжаться сотни поколений или даже дольше. Многие модели, а также эмпирические исследования, показали, что экосистема может функционировать в течение длительного времени в определенном состоянии или режиме (мы можем назвать его метастабильным), но позже она демонстрирует резкий переход к другому режиму функционирования без предварительного изменения параметров (или после изменения, которое произошло задолго до перехода). Этот сценарий, когда коллапс изучаемой популяции происходит без какого-либо очевидной причины смены режима, также называется 'метастабильностью'.
Несмотря на значительное подтверждение наличия длительных переходных периодов в реальных природных экосистемах, а также в теоретических моделях, до недавнего времени исследования долгосрочных переходных периодов в экологии оставались в зачаточном состоянии, и были в основном не систематизированными. Однако за последнее десятилетие был достигнут существенный прогресс в создании объединяющей теории длинных переходных периодов, как в системах детерминированных (т.е. в системах, функционирование которых заранее и полностью обусловлено) и стохастических системах (т.е. при наличии внешних и внутренних случайных факторов). Это значительно ускорило дальнейшие исследования по длительным переходным периодам в экологических системах, в частности, при увеличении сложности рассматриваемых моделей.
В данной работе производится подробный критический анализ последних исследований о длительных переходах и связанных с ними изменениях режима в моделях экологической динамики. Особое внимание в работе таких факторов как экологической стохастичности (наличию шума в системе), эффекту множественных временных шкал (рассмотрение медленных-быстрых систем, с периодами быстрых и меддленных изменений), влиянию неоднородности распределения организмов по ареалу, а также вопросы пространственной синхронизации колебаний численности популяций. Предсказываемая вездесущность длительных переходных процессов подчеркивает необходимость их учета в программах сохранения разнообразия видов. В работе рассказано, как можно моделировать и прогнозировать подобные сценарии.
В работе также обозначена важность использования элементов машинного обучения для исследования длительных переходных процессов. Например, одним из потенциальных способов применения машинного обучения является поиск длительных переходных режимов в сложных экологических моделях, включающих большое взаимодействующих число видов, и как следствие, наличия большое число параметров модели.
Результаты опубликованы в журнале Physics of Life Reviews. Morozov, A., Feudel, U., Hastings, A., Abbott, K.C., Cuddington, K., Heggerud, C.M. and Petrovskii, S., 2024. Physics of Life Reviews Long-living transients in ecological models: Recent progress, new challenges, and open questions. // Physics of Life Reviews, Vol., 51, pp.423-441.
